Inégalité de Fano - Math'φsics

Inégalité de Fano

Formulaire de report
Problème d'affichage Contenu de la note peu pertinent
Inégalité de Fano :
\(X,Y,\hat X\) sont trois v.a. Qui forment une Chaîne de Markov \(X\to Y\to \hat X\)

\(X\) et \(\hat X\) ont le même alphabet \(\mathcal X\)

on note \(P_e={\Bbb P}(\hat X\ne X)\)

$$\Huge\iff$$

$$h(P_e)+P_e\log_2(\lvert \mathcal X\rvert)\geqslant H(X|\hat X)\geqslant H(X|Y)$$

on a aussi la forme dégradée : $$P_e\geqslant\frac{H(X|Y)-1}{\log_2(\lvert \mathcal X\rvert)}$$
Démontrer \((1)\) :

On note \(E\) la v.a. Qui indique s'il y a eu une erreur.

On peut obtenir deux égalités à l'aide d'un diagramme de Venn.

Deux termes peuvent être rapidement majorés.

Un autre terme peut être majoré via la formule de conditionnement par parties, ce qui donne la première inégalité.

Reste à utiliser la formule avec les information mutuelles et le Théorème du traitement de l'information pour avoir la deuxième inégalité.

Démontrer \((2)\) :

Il suffit de majorer grossièrement \(h(P_e)\).

Démontrer :

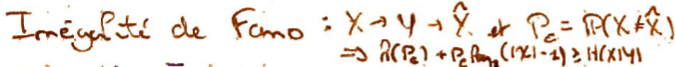
On pose \(E\), v.a. Qui indique s'il y a eu une erreur.

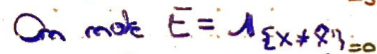
On écrit \(H(E,X|\hat X)\) de deux façons différentes \(\to\) l'un des termes est nul vu qu'on est dans une chaîne de Markov.

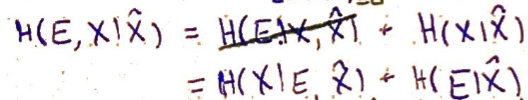
Les autres termes peuvent être majorés en développant selon \(E\), et en retirant un conditionnement \(\to\) cela donne une inégalité intermédiaire.

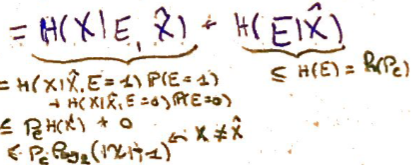
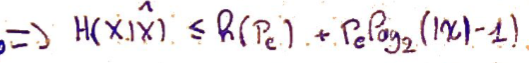
On conclut en écrivant \(H(X)\) de deux façons différentes, et en utilisant le Théorème du traitement de l'information.